第二十六章    傅科刀口检验或阴影检验    M.布朗

 

检验光学零件的许多方法中没有一种方法能够满足所有的要求，每一种方法总有它的局限性。

虽然傅科刀口检验是检验反射镜前表面的第一种实验室方法，但一直只局限于科研方面的使用，直到近今年业余望远镜制造者才广泛地应用它。

1856年，傅科发表傅科刀口检验后，刻勒克斯（ctarks）、布雷歇尔（Brusktr）、菲佐（Fity）及其他在美国的科学家真真使用了刀口检验法。其他著名欧洲光学家，如法国的夫琅和费和卡乔克司（Cauchoix）及英国的塔利（Tutty）在1856的刀口检验法发表以前就制造了大孔径消色差折射望远镜。但是他们所用的方法为了保密而失传了，人们一直认为他们是采用目镜离焦的夏普（Sharn）法，一组消球差物镜形成的圆的等直径和等强度的星点象。

很少有人了解牛顿（1668）和其他人制造的第一台反射式望远镜的经过和他们所用的不同于在夜间用反射镜形成星点象的检验方法。

赫歇尔（Herschet） (1738 – 1822)巧妙地制造了一块中等焦比（F/10 – F/20）的反射镜。只要把参考球面轻度非球面化就可以获得焦比为F/10、孔径48in 的反射镜。他卖出的望远镜大多数具有较小的孔径（6 – 14 in）与焦比大于F/10的球面反射镜，而且可以满足最严格的要求。

牛顿使用上述方法一直到1856年傅科发明用肉眼就可以直接观察到阴影效应的刀口检验为止。

傅科法是在球面镜的曲率中心处在光轴的一侧放一个人造星点，由于反射作用在球面反射镜曲率中心光轴的另一侧形成人造星点的反射象。在曲率中心附近找到反射象以后，可以用刀口来切割成象光束，用另一只肉眼也能观察到一块不规则表面的阴影效应。

在一般情况下，刀口的灵敏度为（0.1 – 1）×10 ^{– 7}in，而且不受尺寸限制，均可以满足高灵敏度的要求。

如果不用刀口检验，就不可能制造出现代的大多数大口径望远镜。显然对大型光学镜面而言，刀口检验是必不可少的，但是对小型光学元件而言，它的应用还有局限性，因为要有相当丰富的经验来判读刀口检验所观察到的不均匀阴影。

自从1970年阿尼桑那（Ariyona）大学光学中心的罗密斯（Loomis）在制造大型望远镜反射镜的过程中推广使用肯特（Kent）单线检验以后（见第二十八章），D.亨德里克斯在帕罗山里克天文台用星点检验法对200 in和120in的反射镜作了最后的修整（见附录16）。

刀口检验的一个重要特点是一般可以不考虑尺寸的大小，检验时，可以一下子观察到整个被检验表面。因此，可以迅速地检测出表面的不规则性，例如象散或非球面性等。

阴影检验的另一个重要特点是物镜支承应达到稳定的状态。若夹持不正确会使大多数精密光学表面产生变形，从而难以保证表面质量。

由于安装镜座时要以前镜面的变形，因此自1939年以来，将大多数反射镜与镜座配合后再安装在为检验而制造的垂直塔内进行加工。帕森 – 格鲁布（Person – Grubb）和阿尼桑那光学中心使用了检验塔后，D.亨德里克斯在天文台内修磨里200in的反射镜。

刀口检验是光学零件的前表面而不涉及到折射，故有很大的使用价值。由于反射镜是消色差的，所以可使用白光。然而，如果系统中包含了折射元件，则需要配上适当的单色窄带滤波器，才能使准直的平行光束有价值。

许多光学元件，例如球面、平面、抛物面、椭圆面以及双曲园锥面和其它光学表面可以用刀口检验，也可以用阴影效应、罗契检验与偏振效应检验均匀性、条纹、气泡和结石。

已经发现刀口均匀对空气动力学及风洞的研究有着广泛的用途。

 

1.  曲面的平面反射

刀口均匀的原理是把光线看作为杠杆臂，被均匀表面看作为系统的支点，使表面的不规则性或不均匀性得到放大。

虽然希望使用尽可能长的杠杆臂，但加长杠杆臂也受到一些，例如检验光路中空气的均匀性和扰动及眼睛分辨表面起伏能力的限制。通常杠杆臂的长度主要由工件的直径决定，工件越大，杠杆臂的长度也越长。杠杆臂越长，由于杠杆的放大作用其灵敏度也就越高。             图26.1   平面反射镜的反射

刀口检验或阴影检验的原理是简单的，反射光线和入射光线以相同的角度位于镜面两侧的同一平面内。如图26.1，图中S为光源、P为平面镜，I为象、J为入射角、r为反射角，光线用带箭头的线表示。

根据实用的目的，一般认为光线是直线传播的，因此,sini=sinr。记住该定律（斯捏尔定律）是很重要的。反射光线以表面误差的两倍偏折，由此决定了阴影检验的灵敏度。

由于光的波长极小，也即为21×10^-6in数量级或近似于对人眼睛灵敏度最高的可见光谱中绿线的波长。把曲面看作由很多法线交于曲率中心的21×10^{- 6}in的小平面组成，这样平面反射光线的特性就可以应用于曲面。

用曲面上的许多水平面来模拟回转面。这就是我们的兴趣所在。光线追迹不可能一比一，而是大大地放大后表示出来。当然必须学会以波长为单位来分析问题。一条直径为0.001in的细线相当于贡绿线波长的47.6倍。

图26.2说明单根光线的曲面反射特性。曲面为SP；曲面SP在Y点的法线为N；S为光源；I为象点；j为入象角；r为反射角。带箭头的线表示光线。实际上，曲面的单根光线反射与平面的光线反射是相同的。                                               图26.2   球面镜的反射

原文误为476个波长 – 译者注。

 

2.  旋转球面

图26.3中的大圆D表示半径为R的空心球体的球面。假设球体的内表面是理想的旋转球面，则c/c点（曲率中心）为正确的球心。如果一个小的球形光源S置于曲率中心处，则可以在整个360⁰方向上反射光线。所有光线以法线方向入射于球面，并沿着原路返回到有原点。球面的内表为旋转球面，所以与用阴影线表示的情况是相同的。                                     图26.3   光源在球心时的球面反射

图26.3的剖面线是顶点S的扇形侧视图。这是用刀口检验回转球面时的典型情况。

由于光线使表面的倾斜误差放大（见图26.4），所以可以观察到球面反射镜的微量表面误差。

由光源S发出的光线入射于曲面E上，然后射到I，r角等于j角，夹角I₁= r+j。用箭头线E点处的斜率变化并记为w，再画出与倾斜面垂直的法N₂

因为S不变，光线S入射到E，由于表面的倾斜，反射象将由I₁移动到I₂。I₁=J+r。当倾斜角w=j时，I₂=2（j+r）。因为j+r为常数，象由I₁移到I₂的移动量为2（Sinw）R。  图26.4   倾斜误差对反射的影响

用I₁、E作刀口检验时，用SE形成I₁角表示正常情况，倾斜变化w时以I₂表示。

现在用一个实例来讨论放大倍率的确定方法。设S到E的距离R（300in），E点的斜率变化W为0.001in，放大后I₁到I₂的移动量以  表示每英寸的弧长值。英寸表示为2WR或2×0.001×300=0.6in

上述问题仅仅是为了说明原理。现在对同一问题以波长为单位来考虑其变化。设E点的倾斜变化为1/2个光圈或1/4个波长或近似于0.000005in，则2（WR）等于2×0.000，005×300=0.003in或是1363.6个波长。用该实例说明如何利用杠杆的放大作用将小的倾斜变化量放大为用肉眼可以观察的量。

大多数测试光学零件的方法都是将微量的误差放大成眼睛可以鉴别的量。

3.  刀口检验的图解

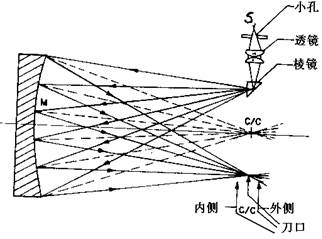
为了研究刀口的功能，大大夸大后画出了图26.5。它由光源S、一对聚光镜和靠近系统光轴的一块小的镀铝平面或直角棱镜组成。远离光源的第二块聚光镜将直径为几个波长的针孔聚焦于反射镜或直角棱镜的前面，反射镜或棱镜将圆锥光束射向e反射镜M。请注意系统中的会聚光路和发散光路。

应注意入射的发散光束的夹角必须大于等于或反射镜M与曲率中心所形成的夹角。若入射光束夹角小于被检验表面M的夹角，则光束不能充满整个表面，因而只能观察到被照明的那部分面积。  图26.5   刀口检验（不成比例）

图26.5中虚线表示原点在曲率中心处的法线，法线与光源发出的光线在表面M上相交，用带箭头的实线表示入射光线与反射光线。

以三个轴向位置表示刀口的位置（图26.5）。首先考虑c/c位置，如果刀口切入反射光线（用箭头表示），表面M将出现一片均匀的阴影，因为由M发出的光线全部集中在c/c的小区域内。当然，这里假设M是理想的回转球面，c/c区域的直径为0.005in。作局部切割时，表面出现一片青灰色。若遮拦更多的光线，则看上去呈一片黑色（见图26.6）。刀口移到图26.5中c/c的外侧，分析后表明，刀口将遮拦与其相对一侧的光线，使该区域内形成阴影，而表面的其余部分则仍然是亮的          图26.6   刀口检验时观察表面M

（见图26.6 b）。

如果刀口移向c/c内侧（见图26.5），阴影将出现于另一侧，如图26.6 c所示。这样就可以决定刀口是否在表面M的曲率中心处。用刀口切割时，阴影出现在水平面上的左边，则表明刀口在曲率中心的里边；反之，阴影将出现在水平面上的右边。出现上述情况时，必须里、外移动刀口位置，直到表面阴影均匀并同时出现阴影为止，这时，刀口必定在曲率中心处（见图26.6 a）

 

4.  刀口的对准

为了对准刀口，观察者必须遵守一定规则，以消除检验误差。见图26.7，图中的虚线办事360⁰旋转时所有平面内的视线（见B、C、D）。如果用双刃刀口则只要旋转180⁰就可以在整个直径的两个方向上进行切割。请注意图26.7a中的E-E，如果刀口以其中一个角度切割光线，则难找到焦点或c/c，而且不可能正确地判读阴影。应该注朝向反射镜中心的切割对阴影的影响。刀口应该调节到与E-E 正交时再来切割光线。

该装置由旋转的目镜托架和优质的10×目镜组成。目镜位于观察者眼睛与刀口之间。为了调节目镜中的象，在c/c位置两侧的水平面与垂直平面内调节刀刃。当狭缝针孔象正好处于目镜的中心时，则为调整良好。对正确的球面反射镜在球心点前后的象说直径是相等的（针孔为扩大的星点象，狭缝为衍射线）。

一台符号使用要求的刀口调整装置由旋转底座纵向导轨、直角导轨和垂直导轨组成。除旋转底座以外都应用螺杆控制，并用          图26.7  刀口检验时的调整

精密螺纹和对开螺母调整刀口。将精度为1/1000in的千分表装于纵向螺杆上，而螺旋夹持在带有叶片弹簧的对开螺母 ，使致能迅速改变位置。

图26，8表示刀口检验的主要部件。所有导轨以小动程自由地运动，同时可用螺钉固紧。刀口可以在3in孔径的圆盘上旋转，以减少象过程中的困难。在目镜的前面还连接了一只小圆盘。

小圆盘用三只直径分别为0 .002、0.004、0.008in的针孔和一个直径的扩展光源组合成。为了用罗契光栅来观察罗契图还用一块有          图26.8  刀口检验装置

1/32in宽度的狭缝的毛玻璃屏，从焦点图到罗契图的定位方向有一定的转换关系（见附录14）。一般情况下用四种尺寸的针孔完全可以满足要求。

对大多数工件来说，需要强光源照明，这可以用一只108W普通电影灯泡来满足要求。当必须检验诸如F/1焦比值的广角光学系统时，则需要更强的光源。图中目镜没有示出，它应该与透镜外壳的托架铰接，同时可自由地绕铰链从原来位置旋出。一般使用10×冉斯登目镜也就可以了，但在有些情况下，需要更高放大倍率的目镜。

对确定光源安装在哪一侧及刀口在水平位置朝哪个方向运动会引起许多混淆。布朗、波特（Poter）与泰塞瑞（Texerau）安装刀口与光源的方向都不一样。布朗将光源放在刀口的右边（见图26.8），刀口及连在一起的光源从左向右运动。波特将光源固定在右边，刀口从右向左运动。布朗与波特提出，刀口应该切割其对面一侧的照明以观察到表面的倾斜。泰塞瑞制订了一个规则：固定光源总是在朝向反射镜的左手一边，从右向左插入刀口。他的判读方法与布朗和波特是一样的。规则适合检验任何光学零件中的反射面。例如（1）带一块平面的自准直装置中修磨有抛物面反射镜的卡塞格林系统的次镜；（2）在带有光学平面的自准直镜中装有一块镀铝的光栏来修磨带校正板的马克苏多夫系统中的主镜；（3）在曲率中心检验凹面反射镜的装置。这样的反射光学系统，光线总是来自于刀口切割的对面。

泰塞瑞规则：一律规定以刀口对面一侧的光束照明斜坡（多被验物镜置于平行光路中时，规则则相反）。检验反射光学系统的三种光学装置均服从该规则。波特装置也有刀口在右边，光源固定在右边的。布朗装置可能会引起一些错觉，因为装置中有一个可以在两个方向移动的狭缝刀口，因而对于光源与刀口刀刃可能产生错误的切割方向。一般来说，人们总是希望用狭缝刀口在右边的方案。

对于透射光学系统如物镜、施密特校正板、马克苏多夫校正透镜、非球面透镜等等，当刀口横向切割时，把光线看作在刀口的后边，换言之，阴影向前投影。

 

5.  检验球面反射镜的前表面

刀口检验时，必须确定针孔或狭缝光源的大小。根据最佳清晰度的要求，理论上光源的尺寸为1×10^—4或5×10^—4in。然而，一般车间里用这样小的针孔是不切实际的，它仅仅是为了满足计量术的要求。

一般使用0.004—0.005in的针孔光源就可以满足清晰度与表面质量的要求。这样大小的光源可以发出足够的光能，使检验单块或多块表面时不致于使眼睛过度疲劳，并且可以达到0.1×10^{- 7}in的精度。

有些操作者欢喜用狭缝光源代替圆孔光源，认为这样可以提高灵敏度并且增加了亮度。

然而，这有一个缺点，那就是用目镜检验象散时，目镜离焦后不可能获得焦外椭圆状图样。

 

6.   衍射

刀口检验时，衍射总是存在的，围绕工件四周可以看到一系列狭而亮的圆环。刀口检验时，衍射并非特别重要，然而初学者可能会混淆。如果用全孔径观察反射表面，四周会出现一系列狭而亮的闭合圆环。最内层的圆环最亮，越向外层圆环强度逐渐削弱，这种现象就         图26.9   刀口检验时衍射效应

是衍射。这是由于工件边缘小圆角或者边缘倒边使光线突然发散所致。靠近斜面顶峰处形成有第一圆环的强度及面积最大，而其它圆环的尺寸与强度均要下降。边缘光线的发散使之分离出一部分成象光束（见图26.9中I）。

可用人眼虹膜作孔径光栏来识别衍射环。观察被照明面时，眼睛向四周转动，当转到某一位置时，在反射镜的亮区域的外边缘有许多暗的光环，即为衍射环（见图26.9中B）。

用刀口切割时，与切割方向相对的一边也可以观察到呈直线的衍射条纹。

在焦点内用刀口切割时可以看到用于确定翘边或塌边的阴影条纹。如果它们的边界位于右边的圆边界上，则边缘塌边；反之位于左边的圆边界上，则边缘翘边。

由此可以看到，刀口检验时观察者可以不必考虑衍射环。希望了解衍射环的人们，可以参阅作详细讨论的光学教科书。

 

7.  视差

视差是傅科检验的另一固有特性。人们曾多次试尝研制一种消视差的共轴系统，但是都没有取得很大成功，因此，观察者必须认识到视差是不可避免的，然而可从找出带区误差的峰值以补偿视差的影响。有关这方面问题在分析有害的带区误差时再做讨论。

视差是由于光源与影像的分离而造成的。分离使入射光束与反射光束间形成了小的角度。

由于有45/45透、反射坚硬膜层薄片及卤素灯源的出现，可以设计出供检验低焦比和R/D小于3的球面反射镜(这里R为曲率半径；D为直径)的共轴刀口仪。

 

8.环带误差

检验球面反射镜时，要尽可能单独检验各种不均匀性及局部误差，以免相互混淆。一般系统中至少存在两种以上的局部误差。在有带区误差时经常出现由各种原因引起的各种形式的象散。有关这方面问题在带区误差测试时再讨论。最常出现的带区误差是塌边。因此，首先讨论这种情况。为了简化，假设球面的其余部分是理想的球面并消除了象散。

为说明清楚起见，需要夸大带区误差及缺陷。

现在可以更详细地解释为什么用刀口可以看出表面的不规则程度。最简单的一个例子是从飞机上向下看太阳斜照的山区(见图26.10)所有受到太阳光直接照射的斜坡将产生阴影。反衬作用使山峰的凸更加明显，从而突出了斜坡的变化。虽然高度是可以计算的，但是反衬作用对高度并不很敏感。

眼睛对它接收到的某一区域的光能量会产生影响。一个有最高的很宽的斜面坡，与真正球面的偏离可能小于几分之一的波长，    图26.10  斜照时用一系列山丘的阴影说明

但是看到的却是一个很宽的高带区。反之，             不同斜面的效应。

具有最低点的一个狭的斜坡，根据光的能量其宽度可忽略不计(见图26 .11中L和S)。因为在L区域有大量的光能，而在S点则只有少量的光能，因而很大程度上要凭经验来解决这些问题。

此外，如果要用刀口检验，则表面的质量应是完好的，不允许存在严重的带区误差。一块制成的优于1/20波长而接近理想的回转球面决不可能出现严重带区误差的效应而使人误测，当然，轻度的带区误       图26.11刀口检验时带区大小的影响

差还是存在的。

 

9.  塌边

图26.12所示是根据中心带区的曲率中心来确定塌边。检验任何反射球面的前表面时，有一条原则必须记住：光源由刀口方向的另一侧照射过来。前述布朗法刀口是从左向右进行切割的，因此，反射镜的斜面从右侧获得照明。                               图26.12刀口检验时的塌边效应

当然，实际上光源在曲率中心附近成象(在左边)，而且为减少混淆，认为光线对表面掠入射，并且入射方向与切割方向相反(见图26 .12)。在反射光学系统中，为了正确地判断明亮与阴影，有一条固定的规则：在图26.12中，刀口置于球面反射镜中心区域的曲率中心处(C/C)该区域内的光线与所有从左边出射的光线被刀口切割，因此是暗的，而从右边出射的光线将通过刀口进入眼瞳，所以右边射的光线将通过刀口进入眼瞳，所以是亮的(见图26 .12)。图26.12中D呈现平面性质，因为在c/c处看上去象平面。同时注意图26.12中C，刀口绕回转环带旋转时，垂直分割亦旋转，故图中表面C中将表面半边翻转。换言之，刀口从左向右切割，如果亮带出现右边缘，则左边缘的带区是暗的，它们是互补的。塌边亦是旋转对称的带区误差，因此左边是暗的，右边是亮的。

9.1要记住的规则

1)     如果刀口从左向右切割(观察者面对反射镜)，光线则从右边射向表面；反之，刀口从右向左切割，光线从左边射向表面，而且全部光线的阴影都倒过来。

2)    与刀口平行一条的反射镜的直径是亮与暗的分界线。分界线的一侧为亮域，另一侧为暗域。

3)     所有面向光束的倾斜面是亮的，背向光束的倾斜面是暗的。

4)    观察者精通这些规则后，就能自然地解释它们。然而必须谨防有时会出现相反的情况。造成这种现象的原因尚不清楚，对视力差的人更为常见。到置的现象使亮区变亮。一般将眼睛松弛几分钟就能看清。令人遗憾的是有时观察者不了解这种情况，因此怀疑观察到的表面质量出现了突然变化，所以在修整前应该作仔细分析。

再假定球面的中心带区是理想的，而边缘翘边。刀口从左向右切割（见图26.13），当刀口在中心区c/c时，刀口切割从右边射来的光线，从左边来的光线则穿过刀口，因此右边暗，左边亮。翘边的斜面或相对中心呈翘边的面，则显示出与图26.12相反的情况，而且从中心区域射出的光线一部分被刀口切割，另一部分则通过刀口，                   图6.13 翘边的效应

因此中心区域比边缘的阴影更亮一些，而且呈均匀变暗的阴影。

第一个例子里，假设不存在过渡的带区，斜面是突然变化的。当然这种现象的罕见的，斜面变化时总会出现如图26.14所示的凹槽。

图26.14A表示有塌边与塌边且内侧有凹槽的球面形成的光线，B是阴影图，C为侧视图，并用平面代替球面。当然，如果表面为球面则不可             图26.14  具有倾斜变化的典型凹槽

能是平的，用点划线来表示球面。另一方面如果刀口置于球心C/C处，则对眼睛而言看上去就好象是平面。图6.14所示并非特例，事实上，这是光学加工中最常见的一种情况，而图6.12及26.13则为例外情况。

图6.15并不是特例，而是作为一条规律来强调。如果刀口从左向右切割，则A是表示光线，B本身就是可以解释的阴影图。

凹槽产生后很难消除，如果需要测量斜面的深度，则可以用刀口检验。大多数情况下，凹槽十分狭，因而要了解C/C与表面其余部分的关系是困难的，所以          图26.15   检验反射面的典型情况

要采取许多预防措施以防凹槽的产生。

应该注意到，所有已讨论过的带区误差是基于刀口位于回转球面中心区域c/c处。然而考虑最有利的情况时，该位置并不是理想的，实际上还存在许多与局部误差有关的其它理想位置，但涉及到许多因素，因而最好根据实际经验来确定。

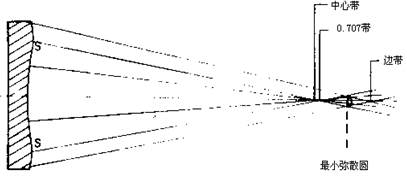
10. 球面象差

所有带区误差的存在，使光线不能会聚于一点而产生球面象差。物和象、焦距及孔径的大小决定了会聚于该点上的光线称之为象差光线并产生球差。每种光学系统均存在一些球差，因此，有象差存在时，靠近焦点或球           图26.16   球差形成的最小弥散圆

心处，使象差光束直径最小，该截面称之为最小弥散园。大多数情况下（见图26.16）刀口应该在平均中心位置c/c点上。

用点划线表示的区域为最小弥散圆位置。

必须用以下三个步骤使刀口置于最小弥散圆位置。

1）     目镜调焦于刀刃的边缘；

2）     调节滑动架，直到目镜里看到的象最清晰。

3）     取下目镜，观察切割情况。

必须记住，并不是在任何情况下都要遵循这些规则。只是在最小弥散圆时提供了表面的平均情况。如果这时球面半径在测量公差范围内（例如在样板半径内），则构成了一种平均切割条件。

假设图26.16中的S-S区域为我们要求的曲率半径带区，则最小弥散圆在c/c右边。

如果反射镜的面形有翘边，则最小弥散圆在所要求曲率半径的内侧或左边（见图26.17）。

 

图26.17  最小弥散圆和翘边时的带区焦点

分析图26.16还6.17后发现，最小弥散圆的位置与所要求曲率半径间的关系是难以捉摸的，应按具体条件决定是否采取最小弥散圆位置。

11. 中心环带误差

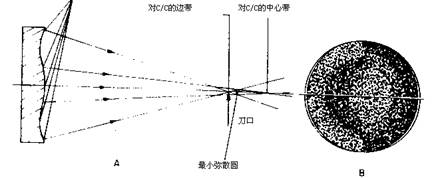
前面讨论的带区误差仅限于边缘带区。现在假设表面的外边缘是理想的球面，而中心区域存在着环带误差。首先研究中心高的（见图26.18）环带误差。

图6.18表示中心为凹区的旋转球面，而且C/C在c/c处。当刀口在外边缘带C/C处，但在          图26.18  中心高的环带误差

中心带C/C内并从左向右进行中间（半）切割时，则表面看上去与图26.16的情况一样，但要注意弥散圆的位置。

图26.19是经常出现的中心凹的情况。注意图26.19中B的焦点图。当刀口在外环带区C/C处并从左向右的中间切割时，外带同样具有阴影，但中心区则相反。同时注意一下弥散圆位置。

以中间切割来作为参考点，这在叙述         图26.19  凹的或中心低的环带误差

上有些含糊之处，因为没有确定切割圆锥光束的刀口的标准或精确的距离。

由于球差（弥散圆）的各种变化和观察者对理想刀口位置的不同看法以及实际的与要求的曲率半径间的差别，要建立标准是困难的，必须根据观察者的经验来确定。

到目前为止，一位新的操作者了解了上述诸问题后，已经可以加工出一个消除了环带误差与象散差并具有正确曲率半径（样板）的理想旋转表面（球面）了。鉴别是否达到理想的表面并不困难，但鉴别非理想的表面则有些麻烦。

迄今讨论的环带误差是一种简单的形式，没有考虑各种各样大小不同的环带完成和象散差。

显然，从讨论中应该认识到防止环带误差是极为重要的，应该采取一切预防措施来限制环带的产生。

较重要的预防措施之一是工件的支撑。工件的表面质量应该与要求的表面质量一致，抛光模的形状及密度分布要对称，避免对一定的动程产生固定的重复的轨迹，特别要注意，一个吸附性好的抛光模只要稍加润滑就能抛出光滑的表面并有清晰的边界。

本文虽然没有涉及到全部环带误差问题，但是对讨论基本的环带误差是有帮助的。

 

12.  象散

毫无疑问象散是精密光学工艺中操作者面临最辣手的问题。产生象散的原因是多种多样的，而且大多数情况下一直到检验时才会发现。产生的原因包括不恰当的支撑，抛光模的不对称性，温度的影响及玻璃密度（均匀性）的变化。玻璃的均匀性包括由于不恰当的搅拌而产生的条纹，结石和气泡。

支撑是只要的。支撑表面必须与要求的表面有相同的表面质量。支撑必须稳定，切勿摇动，而且要将整个表面支撑住 ，决不允许只支撑在一些点上，例如，支撑在腊与沥青制作的点胶上。这是因为光学上使用的玻璃大多具有极好的弹性。

布朗对大于24in的玻璃反射镜的大量生产作过介绍，但没有介绍过用小沥青盘批量生产零件的过程。

加工过程中的对称性，要求工具的变化恒定，除特殊情况外，避免产生不均匀压力。

由于加工，清洗过程中温度突然变化以及高速抛光引起的温度效应可能会时使工件产生变形。

玻璃密度不均匀，例如玻璃各部分的硬度不同也会使抛光速度有差别。

加工高质量表面时必须考虑上述所有这些因素。

由于象散有许多复杂形式，，难以用文字或图解来解释它，而且特别容易与带区起伏及局部误差相混淆，因此，作如下讨论对于过程者识别象散也许有所裨益。当然最好的解决办法是防止象散的产生。

不管球面反射镜质量如何差，用目镜总是检验象散的一种简单的办法。目镜从最佳焦点向内或向外离焦1/32in左右，如果存在着象散，则在最佳焦点两侧的衍射光斑呈小的椭圆形。由这些椭圆象及椭圆平面的位置可以确定象散。一般椭圆的两个主轴互为90⁰ ，但是主轴可以旋转到任何方位。因此，可以由衍射环图样内的两个旋转平面来确定象散。

除了装夹不恰当或全直径上厚度太薄而导致的变形以外，出现象散的最多形式是一个直径方向上出现一定的圆柱形表面。装夹不恰当或厚度太薄，不是由于加工方法而产生的，而是由于加工时支撑工件的方式所造成的。特别是采取不均匀的刚性支撑时，更是如此。

提供给业余望远镜制造者已精密退火过的反射镜毛坯的厚度与直径之比为1/6。布朗制作的200in反射镜中心用沉孔方式以减轻重量（见附录15）。宇宙飞船上in航天望远镜的反射镜采用了一种轻型鸡蛋壳结构，是贝克型三级系统。

 

13. 象散的定性与定量分析

下面讨论中，为了说明问题，假设在一个直径方向出现圆柱形，并且该直径方向的曲率半径大于与其成90 ⁰直径方向的曲率半径。

如上所述，用目镜易于检验表面的圆柱形变。

在图26.10a中用c/c表示短直径，而c图中示出了两对光线。如果刀口置于短曲率半径（KE1）处，水平切割时，在E点看到焦点图。水平面上是长曲率半径的直径，当刀口挡住第一条光线时，发射镜的左边开始阻挡，因而出现暗的阴影。然后将刀口切入轴上光线，则在c/c中心沿垂直直径方向出现阴影带，然后以垂直直径方向向两边扩展并且垂直平分线向水平直径的两边扩展。

适当的切割量，使焦点图的左边是暗的，中心区域稍有些光线，右边是亮的。

图26.20f中，刀口置于刀口2位置，从左向右切割，焦点图则相反，即右边首先出现阴影等第。                       图26.20   象散的效应

如果刀口从右向左切割，焦点图又重新反过来。

图26.20d中，刀口置于平均中心c/c处，或“最小弥散圆“处。为了将表面整个切割到，刀口应该切得更深一些。从左向右切割时，则首先在焦点图的左边出现横穿整个发射镜表面并渐渐向右前进的阴影，如图26.20c中的箭头所示。当然，如果刀口从右向左切割，阴影移动的方向则相反。

再提醒一下，具有最大灵敏度的方向是在与刀口平行的方向，而与切割方向无关。因此所讨论的象散主要涉及水平直径方向的阴影，即与长曲率半径的直径方向有关。

短曲率半径方向的影响很小。这儿讨论的象散效应是定性的，只显示了象散的存在，而不                  图26.21  两次定量测量象散

做定量的分析，否则必须用其它研究办法（见图26.21）。

仍然假设长曲率半径的直径的垂直方向。首先将刀口旋转到垂直方向切割（见图26.20刀口数及a图和b图）。轴向移动刀口至均匀的切割，一般以平均中心c/c内作为垂直直径的零位，然后在仪器上作一次读数记录。下一步将刀口旋转到水平位置并达到最均匀的切割后，再一次读数。两次读数的差值 R近似地等于两个曲率半径的差值。

应该记住，由于切割象散时的位置是不精确的，所以 值也是近似的，然而实际使用上这已经足够精确了。

作为例子对平均c/c点将△ R值分成正（凸）负（凹）数值相等的两部分，这种假设并非绝对正确，但是这种近似性是允许的。

Ast=R ₁―(R₁²―Y²)^1/2―R₂～△(R₂²—Y²)^1/2 (26 ---1)式中,Ast是两个直径方向上曲率半径的差值。若曲率半径R等于100 in，反射镜的半直径为6 in，△R为0.020 in，则

R₁=100—0.01=99.99

R₂=100+ 0.01=100.01

代入后得到h_1、h₂值，h₁=0.18018,  h₂=0.18015,则象散h₁- h₂=0.0003 in，或者象散为1.36个波长。

   因为是用最短的曲率半径求得最大h值，所以取第一个解。

看上去这个问题很困难，实际上只要用矢高公式h=h – (R² –Y²) ^1/2 就可以了。式中h是半口径；y是在球面中心处的深处；R是球面曲率半径。有关这个问题将在以后再讨论。

   因为象散公式中涉及到两种形式的曲率半径（对凹面R₁为负值，对凸面R₂为正值），故把公式分为两部分，独立地解出每种曲率半径h值。

   这种象散型式并非常见，一般只有检验具有球面性误差的光学平面时才如此。象散是一种与旋转带区误差有关的局部误差，因此要分离出象散并定量测定象散的不可能的。

   也可以用目镜的离焦来测量象散。目镜从焦点向两侧离焦同样的值，测量各个椭圆图样的主轴与副轴的长度。由于公式较为复杂，这儿不做讨论。

   精密光学仪器中表面的象散（卷曲面）是不允许存在的。实际上不必讨论象散的全部情况，重要的是在于识别象散的存在。

   刀口靠近c/c时，表示象散的阴影如图26.22所示。在任何情况下象散是不对称的，因而缺乏对称性的阴影图样总是会怀疑其是否为象散。

图 26.22   象散表面的阴影图

用刀口检验象散的另一个问题是对比度问题或者用多少切割量问题。要遵循的唯一规律是当可以清楚地观察到亮区及阴影时即为最佳切割状态。

与象散有关的问题，例如环带不均匀误差，目镜象的判断，曲率半径的定量分析，校正象散的方法及玻璃内部的不均匀（条纹）等全部问题都作讨论则对车间的实际应用而言就太复杂了。但是希望对象散作基本介绍，以便的生产实际中起有效的指导作用。

不要把上述加工过程中的象散缺陷与光学设计中的象散相混淆。前者与成象系统中轴外象点的象差缺陷是有差别的。

用小的非弹性抛光模局部修改不规则或不均匀环带时会产生象散。

附录15只叙述了亨德里克斯和柯旺（Cowan）用小抛光模作局部修磨的，即在金属夹具与沥青胶间加了一层薄的胶合板已获得轻度的挠性。加工小反射镜表面时，用与其同样大小的抛光模，以慢速及1/3动程且不要加压重就可以方便地抛掉象散。对于大型非球面光学零件，在三个区域上用弹簧构成稳定的整体式软沥青抛光模进行抛光已获得成功。压过夜（在抛光模上用了三快液压垫）的整体式抛光模可以自动对中，而且抛掉了不规则的环带，但不破坏已经校正的状态。主轴比一般标准转速（大反射镜为5r/min）稍快些，而且固紧的沥青抛光模有几英m的偏心动程。稍运转一段时间后，就要加抛光悬液。用轻质铝制底模制作沥青抛光模时，沥青抛光模表面应有小网格及方格槽（见图23.8）来吸住抛光粉。网格表面一旦压平，就要重新压制小网格及方格槽。

 

14.    求圆的矢高

下面讨论旋转球面反射镜的前表面，对已知半径和直径的球面求球面的深度或高度。也即在直径方向放上一把直尺，求得直尺到曲线最深部分的距离（见图26.23）。用球径仪测量球面的深度，解出凹面或凸面h值。                   图26.23  矢高深度h

可以用许多方法求h值，下面介绍最符合要求的一种方法。图26.24中标出y为D的1/2，c/c线为R₁Y与R₂间夹角的平分线，并在X点构成两个直角。一个直角三角形用abc表示之，如果弦边绕原点O由S旋转到T，则a= c+h。已知a.c值，则h=a – c. c= a²+b²,若a=10in, b=3in,由电子计算机求得c=0.460678in。

更方便的h值的公式为

h =R—(R²- y²)^1/2    (26 – 2)                 图26.24  计算矢高的原理图

式中，R或a是曲率半径；y为图26.24中的b值。曲率半径为10in，半直径y（见图26.24）为6 in时代入上式。

式（26 – 2）可用于凹面和凸面，图26.25说明凹面反射镜h 值。

如果已知球面矢高h值，则可用下式求得R值。

            R=D² --（2h）²        (26 – 2)

                 8 h

式中， R . D . h 为图26.24中所示的值。

 

15. 求抛物面h值

抛物面是以前表面为工作面的非球面，一般的步骤是首先根据要求的曲率半径制作一个球面，然后再把球面变为抛物面形状。

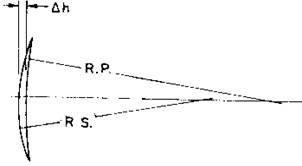
可以有三种方法将一个球面变为非球面。图26.25中，RS是球面的曲率半径，RP是抛物面的曲率半径。            图26.25  球面与抛物面的比较

1） 从四周边缘除掉多余的材料，使球面顶点不变。如果去掉中心部分材料，则抛物面半径变长，但由于焦距变化不大，故在大多数情况下是允许的。

然而在新型的多重反射型望远镜（MMT）中焦距的变大却是一个重要的问题。M.肯特（kitt）原文误为R=D²=（2h）²/8h ---- 译者注。

使用的第一台多重反射型望远镜由六块抛物面反射镜组成。为使或象最佳，必须考虑焦距的变化，为此，可以用第二类方法加工这类抛物面反射镜。

2） 第二种方法如图26.26所示。抛物面曲线与球面曲线在0.707环带相交，图中Rs为抛物面半径。用这种方法制造的抛物面焦距介于第一种与第三种方法之间，但这种加工抛物面的方法是困难的。因为工件上的0.707环带不加工（抛光），因而要修磨狭的边缘环带。虽然这种加工方法去除的玻璃量最少，但却是困难的。

最成功的抛光模是附录14所介绍的玫瑰叶花瓣抛光模。

3)第三种方法如图26.27所示，抛物面曲线与球面曲线在边缘相交。图中Rs为球面曲率半径RP为抛物面半径。

 

图26.26  球面与抛物面的第二种比较法       图26.27  球面与抛物面的第三种比较法

这种方法要在0.707环带内除去玻璃材料，加工后的抛物面焦距最短。大多数操作者欢喜用这种方法，因为不存在边缘环带问题，因而易于加工。

如果焦距为临界值，则在确定初始曲率半径时必须考虑用第二种方法。

众所周知，如第一章所述，入射角等于反射角，在三种方法中焦距近似地等于曲率半径的1/2（见图26.28）                              图26.28  抛物面反射镜的焦点

计算抛物面h值的近似公式是简单的

       h=y²/2R              （26 –4）

式中h为抛物面的深度；y为反射镜的半直径。

   可以用该公式快速近似计算h值，因为抛物面与球面的偏离量很小，一般只有千分之几。

   制作抛物面时，希望知道由球面变为抛物面时必须去除多少数量的玻璃，或者由式（26 –3）与式（26 – 4）求h值。式（26 – 3）和（26 – 4）组合或式（26 – 5）

   dh=R – (R²--y² )^1/2—y²/2R 或dh=h₁--h₂         (26 – 5)

式中d h为抛物面与球面的深度差值。

   如果由球面的中心变形来形成抛物面，则球面h值比抛物面h值小。这是因为求抛物面h值公式是根据图26.29所示的抛物面的变形而求得的，不是由球面h值相减来得到的。

 

15  . 带的视差位移

进一步讨论环带以前，先分析一种重要的象差，即视差位移。                                        图26.29   抛物面h值

视差位移的物点的视见位置与实际位置之间的差值。利用视差效应来确定环带误差的峰和谷的位置，并计算与真正回转表面之间的偏离量。

视差位移效应使视在的高点和低点与实际的高点和低点不同。光源与象之间的分离量，光束的会聚角及刀口周围小量的衍射引起的弯曲均要影响视差的大小（见图26.30）。图中n是光源象的分离引起的视差位移，刀口四周围光束的弯曲是由于衍射所致。由于衍射的影响处于相对次要的地位，所以这种影响可以不考虑。

图26.31表示了视差的影响，图26.31 b中以W和W₁表示视差，图26.31 a中以x表示视差。为了找出环带最高点的位置，要分析视差的最大直径，也即水平直径。

首先从左向右切割，确定其对比度。反向切割时，尽可能保持其对比度相同。根据要求的对比度，用一支铅笔在表面阴影的边缘作上标记,如b图中以S表示。下一步进行反向切割，切割时刀口的进入位置要达到与正向切割时具             图26.30  视差位移n

有相同的对比度，再在阴影的边缘作一记号，如b图中以S₁表示。介于S和S ₁中间的记号即为环带的最高点，b图中的以C表示之。应特别注意：当刀口从左向右切割时，反射镜左边（或切割方向）的阴影向右移动。反之，刀口从右向左切割时，反射镜右边                          图26.31  视差对切割的影响

（或切割方向）的阴影向左移动。

在通常情况下呈旋转环带，不需要在直径的两个位置上作记号，但是要知道对称性图样是相对的，而且，如果需要的话还要找出相应位置的最高点。

再参见图26.31 b 画出W₁环带的轮廓。刀口从左向右切割，阴影边缘S₂，然后刀口从右向左切割，阴影边缘S₃,则最高点C₁点。阴影随切割方向而移动。

总的说来，这些方法适用于“单一”前表面的反射镜。对于多次反射和透射的情况，阴影或亮区的位置则有所不同。但是，用上述所介绍的方法可以找出最高点或最低点，再根据经验可以解决所有的问题。

因为不同情况下视差是不一样的，重要的在于知道它的存在。直径12in的反射镜，单向切割时月.0.5in的位移，或者在两个方向切割时总的位移为1.0in亦不罕见。

这是焦点图的定性分析，附录14叙述了罗契图的应用，并说明了共轴检验时，用焦点图与罗契图的相互变换可以消除视差位移。用刀口焦点图变为罗契图需要一块大的狭缝和小的罗契图光栅。用一块相当粗但80e/in的小光栅可由眼睛观察到罗契图并应用软铅笔在坡度变化的最高点作上记号。

另外一种方法是用单丝或双丝测试法。在刀口狭缝上放一根单丝（用一根头发丝），然后在任一环带位置观察弯曲的罗契线，就可以显示视差位移（见第二十八章）

 

16． 带差的测量

只有表面满足下列条件时才能定量地测量环带差。平均中心是球面的中心，环带的过渡区必须由球面光滑地变化而或不存在深的凹槽和高峰状的突变环带差。定量测量时应利用讨论视差时所述的方法仔细地找出环带区的最高点，最低点及环带宽度，环带的宽度是计算环带误差的一个重要因素。

图26.32  表示了三种不同形式的环带差，表示过渡区环带差及不旋转对称的环带差。检验环带差A和B是困难的或者是不可能的，而C处的环带差应该是标准的，这种环带差可能是塌边或翘边引起。中间带是低带，高带或凹陷的环带差。

环带差的计算公式为

Δh=(yΔR/R² ) (W) （26—6）

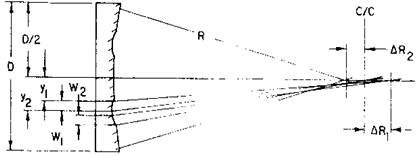
对单个反射镜，Δh是环带相对球面的偏离量；ΔR是环带光线与光轴的交点与平均球心c/c之间的差值；y是轴到边缘的距离；                      图26.32  表面的环带差

W是环带的宽度。

 

17.   塌边

作为例子来分析图26.33塌边的情况，球面直径为16in；曲率半径为100in。下面的讨论均用上述这些常数。

假设塌边是旋转对称环带差，已用刀口找到了最高点并用y表示之。对W或0.2in的环带宽度作了5次测量，其算术平均值为ΔR                 图26.33   塌边的环带差

现在考虑误差值Δh, Δh = yΔR/2R²(W)，用0.000022in（波长值）除以0.000024in求得该环带有1.14个波长的坡度误差。

18.  中间环带差

图26.24表示一段中间环带，y₁.W₁和ΔR是测量处。该环带差由两部分组成，因此需要计算旋转环带差的两个半部。

对该环带的分析表明，如果用W₁表示的表面比球面更凹，则另一侧用W₂B表示的比欲达到的                    图26.34  中间环带差

球面具有更大的坡度。因此，两部分均要计算，然后取这两部分的算术平均值。

Δh =(y₁ΔR₁)/R²(W₁)+(y₂ΔR₂ )/R₂(W₂)          （26 – 6）

式中，y₁为4in;R为100in;W₁为1.5in;y₂为5.5in;W₂为-0.02in;ΔR₁.ΔR₂取5次测量的平均值。

ΔR=（y₁ΔR ₁W₁/R² +Y₂ΔR₂W₂/R²）/2

则总的变化受.000012- 0.0000142in,也即该环带的误差为0.78个波长。

 

19.  中心高或低

中心区域产生环带差时，则y和w的测量值完全不同（见图26.35）。这是                 图26.35   中心高的环带差

y是光轴到环带边缘的距离；W是环带边缘到光轴的距离。适用于高.低区的公式为

Δh=(yΔR/R²) (W/2)                       (26 – 7 )

式中，y为4in.将这些数值代入，然后计算求得Δh为0.000008in大约受.04个波长。用同样的方法计算中心低的带区差。

 

20.  焦外刀口检验

焦外或曲率中心内的检验（罗契法）是刀口检验的一个重要方面。

这种刀口检验法的应用类似于罗契检验。刀口形成的单边图样类似于罗契图样，它对环带差的起伏是灵敏的，但是不能作定量测量。如果在平均曲率中心c/c处将刀口检验法与目镜检验法联系起来，则可以获得有用的数据。

刀口在平均球心点c/c内侧切割时观察到的塌边现象为第一种情况（见图26.36）。下面仅考虑焦内切割情况；刀口置于中心带区c/c点内侧约0.125in处，图26.36中的阴影边缘表示了单丝以不同的程度来切割中间带区。

整个反射镜出现阴影时，由于塌边的影响，F处焦点图在垂直平面内出现稍凹的图形。切割量增加到y时阴影的中心区域朝中心线弯曲。因为塌边是弯向中心线的曲线，因而实际上塌边深度焦点图是曲线而不是直线，在F处阴影边缘是凹的，当面向反射镜从左向右切割时，该区域的光线向左边反射。然而，当阴影进入球面区域时，因为光线会聚于一点而且又均匀地分布于切割区域上（见图26.36C），故边缘             图26.36  刀口置于曲率中心内时观察到的塌边现象

就变为直线。

如果继续进行切割，直到阴影边缘超过垂直线后，阴影末端则反向垂直线，如图26.36中.k所示。如果阴影I和I是实线，则它们就形成这种环带形式罗契检验的特征阴影图。

21.1  翘边。

边缘的翘边形成情况与上述         图26.37  刀口c/c内时观察到的翘边现象

相反。图26.37的F处产生阴影时，首先出现的阴影稍为有些凸，或者的阴影进入到球面区域以前，水平直径方向的焦点图弯向于垂直线。的球面区域内阴影为直线。在图26.37y.h和j位置上，带区的阴影背向于中心线弯曲。阴影过中心线后，i.k处出现阴影。如果i.j区域出现阴     图26.38  刀口c/c之内观察中心低带差时的现象

影，则为翘边罗契图样的特征阴影图。

必须记住，环带误差的大小决定了阴影变化的大小。如果环带误差我几条条纹，则阴影的变化明显。环带误差缩小时，阴影的变化也跟着减小。

21.2  中心低

中心低而外边缘为旋转球面，则的阴影进入到误差区域前，阴影的边缘是直线（见图26.38）。当然，阴影通过中心线以后，阴影线将以相反方向弯曲。i和j是阴影，则形成中心低的罗契图形的特征图样。

21.3  中心高

自然中心高与中心低是      图26.39  刀口在c/c之内观察中心高带差时的现象

相反的，在球面环带区域内，由y 到j，阴影为直线（见图26.39）。如果i和j区域存在阴影，则为中心高的罗契图样。

前面讨论环带象差的例子，说明直边形成阴影时环带误差对边缘形状的影响。用直边切割由旋转球面反射的光线，从而可找到环带误差位置。当刀口置于平均中心点c/c时，也可以用阴影来论证许多情况。

虽然的前述例子中讨论单个环带的情况，但两个或多个环带差同时存在时，上述的讨论是有效的。用阴影的形状来确定坡度变化的分析方法对所有情况都是适用的。

几个环带差同时存在时，阴影可能变得复杂。当然，精密加工中必须消除严重的误差。

阴影图的价值在于分离出环带误差，以便作局部修磨或估测出环带的位置。

应该提醒一下，当用刀口在平均曲率中心处切割时，这种情况下的阴影检验对有象散的表面是不灵敏的。

用刀口刃边作罗契检验时，并不能认为是一种真正的罗契检验，因为它只采用了一条线。

如前所述，在扩展狭缝光源上只要放一块光栅，则刀口仪可以作为罗契检验仪。附路12和附录14叙述了单个带差和两个带差存在时的罗契图。

 

22． 非球面或园锥面

经常使用的旋转非球面是抛物面。下面讨论检验这种表面时应该考虑的一些问题。

前面几章中已叙述了旋转抛物面及大多数操作者更欢喜使用的变形球面中心区域形成抛物面的工作方法。以此为基础，评述抛物面的检验。

确定抛物面质量有几种方法。例如零位平板检验法；在平均曲率中心或者表面曲率中心处放一块平凸透镜的零位检验法(Dall)；用目镜的星点检验法。

一直到傅科发明刀口检验以前，夏普、牛顿和其他科学家均用上述四种方法中的目镜检验法或用检验非球面象质的方法。

星光是发射出平行光束的光源，可以用目镜检验象质，但这并不是一种高质量的满意的方法。因为目镜主要用作“切割和校准”，因而，专家们提出了一种焦内、焦外检验影象的精确方法。如果反射镜的焦内、焦外园环是相同的，则该透镜系统的校正是良好的。

参阅D.马拉卡拉主编的《光学车间检验》（Ed.Wiley,New York,1978），威尔福著的关于干涉检验、刀口检验和单丝检验的单节。

随着刀口检验的出现，检验情况有了很大的进展。克拉克首先使用零位平板检验，而德雷珀及菲佐可能相形见拙。当然，前者需要一块高质量的光学平板以形成平行光束，但却是确定表面质量的最简单的方法之一，而且在平均球面中心c/c处同样可以简单地测量球形表面。检验抛物面与检验球面的差别在于检验抛物面时是在焦点处进行测量的。

 

23．零位检验的牛顿法

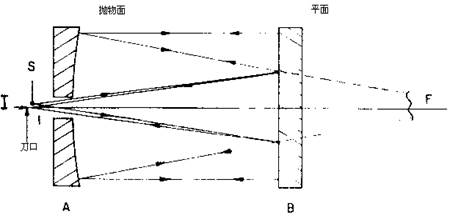
在图26.40中S为刀口；I为象；D为反射平面；A为抛物面；B为平面。从光源出射的光线经D、A到达B。由B平面反射的光线从相同的光路聚焦于I。P处的虚线表示制成抛物面前的球面。制成抛物面以后的表面与球心在c/c的球面具有同样的平滑情况。反射镜产生的无光死区是不重要的，因为在光学系统中通常不采用它。45⁰反射镜D使光源与刀口置于抛物面与平面间的光路之外（见图26.40）。因为光源在光路中会产生扰动，所以这样布置就很为必要。           图26.40  零位检验的牛顿法

用星点光源取代平面反射镜，则成为标准的牛顿望远镜。

应该强调一下，在自准直光学检验中，用刀口检验可以得到扁球形焦点图（见附录14.2），图A14.2为罗契图。

在图26.40装置中应考虑二点：第一，在45⁰反射镜后面应放一块直径比它大三倍以上的光学平板，否则在曲率中心观察不到自准直象（见图25.8b）。第二，保持反射光源与反射镜中心精确同心，否则会观察到象散焦点图。

24．卡塞格林的零位检验法

通过主镜中的孔可以检验卡塞格林装置中的抛物面（见图26.41）。

在这种情况下，平面反射镜既作为由光源发出的发散光束的反射器又作为平行光束的反射器。如图所示，光源原点S经B反射投射于A，然后再返回到B并以同样的光路返回到I。这实际上是              图26.41  卡塞格林的零位检验法

一种双叠光路的反射系统。

由切割面形来验证抛物面的表面质量，该方法的优点是仪器结构紧凑。如果反射镜未修磨好，则刀口焦点图将呈扁球形（见附录14）。

 

25．第三种零位平面检验法

检验抛物面的另一种装置如图26.42所示，平面反射镜中心有一个孔，形成另一种型式的卡塞格林系统。

图26.42  第三种零位平面检验法

平面反射镜蹭的孔作为光线的通光孔必须足够大，这种装置也很紧凑。平面反射镜的中心孔使抛物面中心存在一个不可能被检测的死区，但是在抛物面中心，如果孔太大会引起表面变形，因此在表面中心区仍然有质量要求。

用上述方法之一可获得最高的精度，但需提供高质量的平面。

如果抛物面的相对孔径等于或高于f/3，则可以用戴尔零位检验法。用一块平凸透镜和置于一定距离的红色滤光片组成检验装置。这种检验方法在纽约Scientific American出版社1953年出版的Amateuw Telescope Making 第三册p149有详细叙述。这本书是再版的，书中载入有经验的业余望远镜设计者及光学家，如詹姆斯、G .贝克和D.亨德里克斯的有关文章。

记住第二十四章所述注意点，必须使刀口与光源靠近，以防产生轴外象散。

26．离轴抛物面的零位检验

检验离轴抛物面的呼声逐渐强烈，刀口检验是测量表面质量的最实用方法。现简要叙述如下。

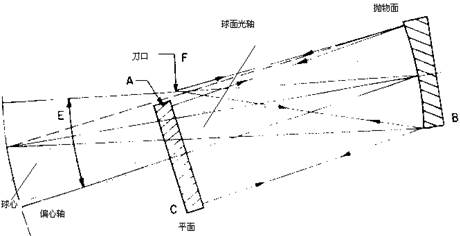
图26.43说明其原理，刀口置于A；球面的轴外焦点用虚线表示；D为偏心角的平分线；E为偏心角。位于偏心轴上的平面反射镜使从B出发的光线法向入射于平面反射镜。                 图26.43  离轴抛物面的零位检验

箭头表示光路走向，虽然仅表示出了一半光路，但可以将光线折回系统，完成整个光路。

再用刀口对面形作光滑的切割检验，得到一块好的离轴抛物面镜。

检验时应考虑一些关键的要求，但是，首先要确定变形的性质。

采用旋转对称的变形把一个球面转变为旋转抛物面，但是在制造离轴抛物面时，则破坏了表面的对称性。表面顶点的移动量取决于偏心量，顶点从球面中心移到偏心   图26.44  离轴抛物面零位检验中用球面的检测结果

平面内偏心方向的另一侧。

开始修磨以前如图26.44所示，z表示球面；x处的虚线表示用刀口校正以前的球面；y近似地表示表面加工后的形状，当然这是大为夸张的画法。

图26.44B的焦点图类似于离轴的特殊表面。当观察者面对反射镜从左向右切割时，阴影区域表示为中心高，并表现阴影延伸到垂直中心线的右边，系统中因失对称而使表面顶点移位。

很明显，这种形式的变形，使完工后的表面不可能成为一个旋转的回转表面。因而，重要的是检验时，反射镜必须精确地放到原来的位置与方位上，为此反射镜四周应做上固定的不同记号，并使反射镜精确地定位于指针的镜座里。

出现如图26.44B所示焦点阴影图的形状仅表示存在着变形。对比的高低取决于镜面的f数及偏心量。最显著的特点是其中心明显地高出，而且顶点稍偏向于垂直平分线的一侧。同时也必须注意观察焦点两边的罗契图。

第二个重要的问题是确定应该去除多少材料。因为不能用回转表面形成离轴变形，而是必须用小尺寸的工具来修磨并通过检验确定应在什么地方修磨。

可以设计一种加工这类表面的机床，但是太花费时间，因此并不合算。

阿里桑那光学科学中心已对此作了一些改进，但是很少有报导。

在此叙述的是一块直径大于10英寸的反射镜，更小直径的离轴抛物面反射镜通常是从一块大直径抛物面反射镜上套钻下来的。

 

27．在曲率中心检验抛物面化的程度

用这种方法检验抛物面有许多优点与缺点。优点是：不需要优质的平面，也不需要每次进行反射镜的对准而且又不受尺寸的限制。

缺点是：检验表面时要用小孔径环带光栏，而且要用一块可以同时观察整个表面的模板。用等比法来确定各个环带的曲率中心时需要操作者有一定的技巧，结果处理时涉及到一些数学问题。但是，用这种检验法的花费小于制作一块1/20波长的光学平板。用这种方法检验的抛物面，其质量表面大多数可以满足要求。

检验过程中，根据第十四章所述方法使抛物面与球面边缘相交（见图26.25），再将球面变形为抛物面。边缘环带是重要的，因为边缘狭带是加工抛物面的参考环带。

如果中心区有0.6环带差，则用星形线延伸到边缘的星形沥青抛光模（参阅附录14）。但是使边缘环带有精确的曲率半径、消象散而且没有塌边。这种制作抛物面的方法并不会使焦距缩短。

将一块1/16英寸厚的足够大的卡纸或硬纸板制成一块卡板。硬纸板的园盘尺寸与反射镜的直径要一致。如果抛物面有深度弯曲，则必须用水将硬纸板浸透，然后弯成反射镜的曲率，最后再放在反射镜上。下一步是将全直径磨模放在硬纸板上，使之干燥。两边滴上虫胶，并涂上两层烟黑，使凹面有合理涂料，以使硬纸板的形状保持不变。

然后把园盘剪成反射镜的大小。

准备开孔，孔的大小取决于曲率半径。如果曲率半径大于50-60英寸，而孔的直径小于0.5英寸，则是不恰当的。因为衍射效应限制了有效孔径的大小。曲率半径为60-120英寸时，孔直径为0.75英寸。曲率半径大于120英寸时，孔直径近似地等于曲率半径除以225。例如，半径是300英寸时，开孔为300/225=1.3英寸。并不是一定需要这样大小的孔，对有经验的观察者，可以采用1英寸大小的孔径。

图26.45为标准模板的设计。根据孔径、间隔及同心度的相对尺寸，尽可能精确设计。可以用锋利木钻将背面衬上光滑松木板的硬纸板作成孔          图26.45  抛物面c/c检验的模板

径板，孔钻出后，边缘应涂黑。

图26.45中的D为反射镜直径。安装模板时，必须与光轴同心，并与反射镜的表面接触。决不允许脱开。

孔间距应使孔边缘之间相距0.125英寸。

如果要求的表面质量很高，则用两块模板，第二块模板孔中心距为第一块模板孔中心距的一半。

图26.45示出了水平直径方向上的开孔。为了减少观察者的视觉疲劳，应在最小变形的直径方向进行测量。由于玻璃的不稳定或不恰当的支撑而产生变形时，一般在垂直直径方向上影响最大而水平直径方向上的影响最小。

在可翻转的机床上作立式检验时，大反射镜支撑在反射镜四周围的一条宽度为反射镜园柱宽度一半的钢带上（见图2.29）。实际上，制作大反射镜时，采用垂直检验塔将反射镜与支撑望远镜座的托架连接在一起，有关镜座托架参见附录15。

28．环带偏差的计算

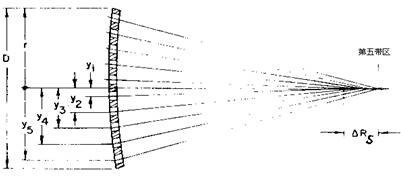
图26.46表示位于纸平面上模板的水平截面，模板放在反射镜前面，图上的间隔是夸大了的。

用△Rs表示抛物面，球面上所有环带的R是相同的，不应该有△变化。图26.46所示的光锥只表示出反射镜的一半，并标志出检验抛物面的5个环带孔（1-5）。               图26.46  确定反射镜的环带偏差模板

△Rs是光线与光轴的交点位置的变化量。用y₁、y₂……y₅表示模板上环带仅一边的测量值，（图26.46仅表示出一边），例如y₅和y₅形成一对，以后再来说明其测量方法。

用△Rs测量值度量反射镜表面在该点上的斜率变化。由于表面的起伏使反射光线交在c/c处及其附近（见图26.47）。

参见第14节图26.28，该图表示了理想的表面其所有反射光线交于曲率中心一点。我们也要学会从最边缘（参考带）着手磨制抛物面，并用所谓“曲率中心检验”法来检验抛物面。               图26.47  反射镜面的环带误差

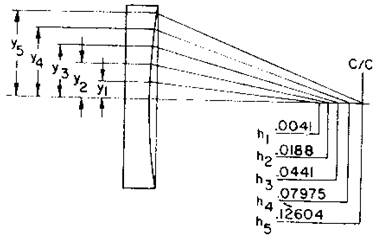
29．模板的应用及h值的计算（见图26.46）

1．）位于反射镜前面的模板将反射面分割为许多园形环带。对理想的抛物面，由y点的计算值来确定锥光束与轴的交点。如果抛物面不完善，则用计算值与理论值的差别来表示表面误差，△Rs求和后，以波长为单位作出表面误差图。

大多数业余望远镜制造者害怕用数学术语，实际上只要将最后数据表格中的最后两行交叉后代数相加即可。下       图26.48  反射镜5个环带的△R值

面会作更详细的说明。

2）假设反射镜直径为12英寸，曲率半径120英寸，抛物面焦距60英寸，反射镜是理想的球面。模板上有十个1英寸的园孔，每个孔的边缘之间相隔为0.125英寸，则孔的中心和抛物面的计算值如表26.1所示。

表26.1  第一步操作（英寸）

第4列是第2、3列之差值，第6列是第4、5列之差值。

第5列为抛物面纵坐标的计算值。

第6列是△R测量值。

3）用前述式（26-4）求矢高或沿反射镜光轴方向抛物面中心的h值。抛物面公式（26-5）为： 

用刀口与光源一起移动或光源固定，刀口移动的方式来测量环带偏差

                     h=y²/R                    （26-6）

式中h是抛物面值；R为曲率半径。注意抛物面的h为式（26-5）中h的两倍。

用式（26-5）时，y是光轴到模板孔中心的距离。当R为120英寸时，y的测量值列表表26.1。

4）现将抛物面的纵传标值列于表26.1，通过计算求模板开孔（1英寸）处的斜率。用白墨水在模板开孔下面记下每次抛物面纵坐标的计算值（见图26.48）。

5）图26.48中，曲率中心处刀口对边缘环带或y5(0.126in)带的移动量为h，它是一个逐渐减少的量（每个环带间的真正差别）。若以y5环带为参考带，则所有的测量值以它为基准。

例如，假设刀口在y5环带的曲率中心处，则到y4环带的交点，刀口应向反射镜移动多少距离呢？该量应该等于0.12604-0.07975=0.04629英寸。h4到h3环带刀口应向反射镜移动0.12194英寸或者大约为1/8英寸。

在此必须指出，外环带的测量值必须十分精确，否则因中心环带的会聚角变小使中心环带测量值变小，从边缘到中心的环带y5误差减小，从而测量误差增大。相反，由于近轴带区（中心）不存在误差，也使边缘带区的误差超差。实际上，中心带区0.005英寸的误差是许可的。

6）最后用方程（26-7）计算斜率。如果误差有正负，则种种误差相加时，可以彼此相消。

除非小孔的大小是1英寸，否则必须将△R差值变换为各个小孔直径上的斜率误差。

斜率误差与三个因素有关：

(a)制作抛物面以前球面的曲率半径。

(b)列于表26.1中的每个环带y的计算值。

(c)抛物面纵坐标的计算值。计算公式为：E=(yd△R)/R²       (26-7)

式中y为环带模板小孔的中心距；d是小孔的直径（模板的d为1英寸）；△R是抛物面的纵坐标与刀口测量值间的差值；曲率半径R为120英寸。

7）在刀口的轴向螺旋上啮合一个精度达到1/1000英寸的千分表，当刀口远离参考带区y5时，该读数值减小。

计数器上的读数可能是7543或2345。调零后读出的数应大于抛物面纵坐标的最大计算值。如果刀口仪上没有带数字千分表，则可以另外加一只有足够行程（0.126英寸以上）的千分表。

对5个环带的每一个环带取5次读数的平均值，并画一张类似于表26.2的表格。y5环带的刀口读数从8.675开始，用8.675减去修整后抛物面y5环带的值0.126得-8.549（注意小数点的变化）。如果没有标注变量为负数，则不能决定测量值是正值或负值。

作表26.1后，用表26.2求和。F/5、12英寸抛物面反射镜应修整到面形误差小于一个波长。

表26.2  第一次操作求和

*：Σ为求和，例如0.115+0.096=0.211， 0.288-0.049=0.239

8）用星形抛光模进行第一次抛光，由表26.2得到图26.49a中以波长表示的小数值。实线表示作光滑曲线的值，虚线表示继续进行抛修时的变化。注意在图26.49a中如何用虚线画出X端，并以y5带为固定点作一个不作任何抛修的矩形框。曲线的斜率表示用星形抛光模精确加工出来的抛物面。图中y2为最高带区。

 

30．改进抛物面第一次抛修的措施

抛物面的衍射极度限是1/20波长，用同样的星形抛光模作进一步的抛修以减少△R值，一般应小于0.5波长。y5环带的和数是0.000；y4是0.057，y3是0.100，y2是0.134，y1是0.157波长。用图26.49b曲线表示第二次抛修后的和数。当环带y5区域不作任何抛光时，注意用虚线画出的端发生偏转变化。图的曲线形状表示用抛光模精确加工成的抛物面。                  图26.49  抛物面的抛修过程：

a)按表进行第一次抛修；

b)第二次抛修；c)完工后的抛物面进行第三次抛修

第二步操作后使△Rs减少到0.5以下，其修正量大于第一个曲线形状（见b图）和数误差的一半。

该过程与实际操作是一致的。要加速将球面变为抛物面，必须从实践中获得感性认识。

如果要制作1/20波长的抛物面，则△Rs必须进一步减小。这可用同样的星形抛光模来达到（虽然可能性是很小的）。在c图上作一个假想的操作曲线，使△Rs值减小到接近精确的值的测量极限。

甚至用布朗方法测量△Rs也存在困难，但是用固定光源和移动刀口是可以克服的。这里给出两倍的△Rs值：  h=y2/R        (26-8)

式中h,y,R与式（26-6）及（26-7）一样。

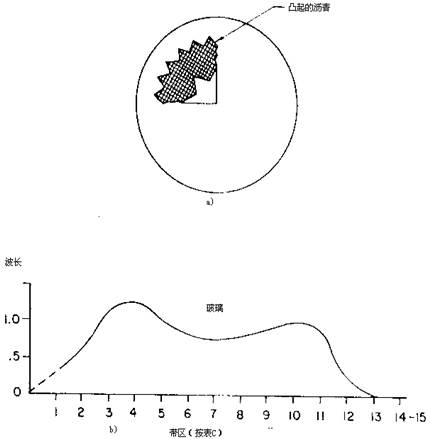
31． 大孔径抛物面的光学检测

画一条f/2.97大孔径（30英寸）抛物面反射镜的面形误差曲线是有意义的。该表面有一个波长大小的斜率缺陷，而且还有许多离散的中等大小的斜率误差。

图26.50a表示带差为1.3波长（见表26.3），说明可以将抛物面反射镜再抛光成为球面，但这是不切实际的。如果画出抛物面曲线并用特殊的沥青抛光模来抛修抛物面，则可以很好地达到光学面形的要求。

初学的操作者及业余望远镜爱好者感兴趣的是如何修正该表面及加工过程中会出现些什么问题。首先研究什么形式的抛光模会使这个表面磨坏？加工抛物面过程中必须用直径大约为12英寸的星形沥青抛光模，抛光模吻合性差时，可以采用干抛光。     图26.50.  反射镜的斜率误差（见表26.3）

根据图26.50的曲线仔细地修磨

斜率误差。还要注意两个凸坡，并用环形抛光模除去。在环带4和10的凸出处加大抛光模的抛修量。抛光模上加制的小网格是为了保证抛修时接触良好。抛光模用2英寸的动程并在反射镜上作慢速抛光，主轴以20rpm的速度旋转，摆轴以大约20rpm的速度旋转。

表26.3    环带1英寸

表中：f/2.97  30英寸抛物面  R₀=178.281英寸  2R₀=356.57英寸  f=89.14英寸  R₀²=31784.9英寸²。

y  标注在反射镜上的每个环带孔的高度。

R₀  中心区域的曲率半径，抛物面纵坐标PO。

y²/2R₀  法线与反射镜中心轴交点的理论偏差（见图26.50）（注意光源与刀口在一起）。

△L  政论值与实际千分表读数间的差值。

e  每一环带内边缘相对于法线的高度，假设外边缘是正确的，公式是e=ydL/R²，这里y是环带距离，d为开孔直径（1英寸），L为环带差值，R₀²=31784.9。

d  模板有13个孔的开孔环带宽度。

Σe  环带高度之和，注意每个和数与下一环带交叉地相加。

λ  反射镜在y环带上的角误差（见图26.50a）。

32． 卡塞格林次镜的自准直检验

卡塞格林望远镜的副镜是双曲面，主镜为抛物面。

通常先按预先计算出的球面反射镜研磨和抛光双曲面次镜，然后将它与抛物面组合成平行光管装置后再来修磨之。刀口检验给出平滑的焦点图，如果副镜已真正地修磨成为双曲面，则由罗契检验得到一组等间隔平行线的罗契图（见附录14，图A14.1和   图26.51是检验双曲面次镜和抛物面主镜的常规装置。

A14.2）。在如图26.51所示的光学装置中放上球面次镜后，则刀口的焦点图或罗契检验是结果是一个扁球形。在这个光学检验装置中用0.707直径玖瑰叶花瓣抛光模修磨扁球形来达到零位检测的要求。

因为象太暗淡，所以应该将主镜镀铝。

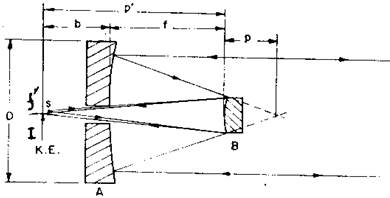
图中A为主镜，B为次镜，C为镀铝平板，组合反射镜的焦点在f’，I为刀口，S为光源，f为主镜焦距，P’为从双曲面到系统焦平面间的距离，               图26.51  副镜的检验

P是双曲面到主镜焦点f’的距离。

首先设定主镜的直径及焦距。假设主镜直径为12英寸，焦距为30英寸。

其次选择放大率为4（在式（26-10）中骼A表示），则：

        P=b+f/(A+1)                  (26-10)

式中，P是主镜焦点内的距离；b是主镜顶点的后焦距（一般为主镜直径的8/10）；f为主镜焦距；A为系统的放大率，则P=（10+30）/（4+1）或8英寸。

次镜直径是12/30*8=3.2英寸，实际直径大约为3.5英寸。由式（26-11），曲率半径为：      Rc=(e+1)P        (26-11)

式中e=A+1/A-1。如果A为4， e=5/3=1.666，Rc=2.666*8或21.328，整个焦距为30*4或120英寸，该系统是f/10。

主镜中的孔必须足够大，认使其与检验时的入射与出射光锥相适应。对于这种尺寸的主镜，孔的直径取3.5英寸可以满足要求，从主镜上钻下来的玻璃可以加工成次镜。

 

33．用侯德尔法检验次镜

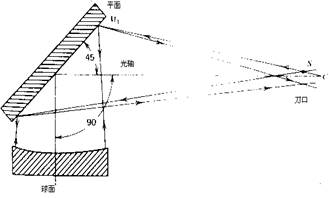
侯德尔法是在抛物镜处放一块比主镜稍大些的球面镜，球面镜的曲率近似等于主镜的焦距。反射次数从图26.52所示卡塞格林装置中的6次变为图26.53所示球面装置中的3次。在A.I.英格尔斯编的《业余望远镜制作》中可以找到有关侯德尔文章更详细的资料。

图26.52  用侯德尔法检验卡塞格林系统。

图26.53  球面的侯德尔检验法

这种检验方法或用于理奇伟-克里蒂设计的望远镜次镜。该系统有两个双曲面反射镜，主镜也是双曲面，国而比常规卡塞格林系统的视场大。

 

34． 平面反射镜的刀口检验。

用刀口检验平面时需要一块标准球面。

标准球面必须具有很高的质量及长的曲率半径，如果R为被检验球面的曲率半径；D为其直径时，一般R/D为20时已经足够。

虽然从球面只反射一次，但共有三次反射。球面所有的误差在系统中成倍地反映出来，故球面的质量是重要的。球面不应存在看得见的带差，用刀口切割时，球面镜不存在象散而呈现平滑、均匀的阴影图并应镀有高反射率的铝膜。

经过仔细地检验反射镜，并镀上均匀的高质量铝膜后安装在镜座里时不得引起变形。如果所用的平面是高质量的，在曲率中心处直接观察时，球面镜的孔径内应没有明显的带差。两个零件的镜座结构应牢固，并可以作对准调整。从长远观点看，采用临时性的装置是不合适的。

图26.54表示用球面检验平面镜的一般装置，刀口位于S，测量c/c到M1和M2的距离为曲率半径。

阴影图中的亮和暗的判读与在球面曲率中心处直接观察球面的结果是相同的。它们间的差            图26.54  用球面反射镜检验平面镜

别是前者的旋转刀口可以关垂直

方向和水平方向两个方向切割。如果是用理想的球面与平面构成的，则刀口旋转到任何位置时，阴影都是均匀的。然而难以获得两块都是理想的反射镜。如果反射镜具有轻度的正或负（凸或凹）误差，则会导致系统中出现球差。由于是三次反射，所以灵敏度很高，球差就很容易发现。

上述内容中已涉及到阴影的判读（见附录14），但是有一个值得注意的情况：这就是在水平面内以45⁰方向观察时，平面反射镜将呈椭园形。

 

35．平面曲率的确定

与球面比较，测量平面的曲率比测量球面更为复杂，因为共有三次反射，所以在平面的45⁰方向测量时会有极度高的灵敏度。

通常可以使平面反射镜与系统光轴成精确的45⁰角，以便可用简单的公式不计算。然而，如果不可能构成精确的45⁰角，则角度以及顶点到平面反射镜顶点的距离也应该为已知值，而且误差应在0.25英寸以内。

首先列出基本公式，然后简化运算

h=0.03125(D/R)²(COSθ/SIN²θ)(△RR/(R-S))          (26-12)

式中，h为正负偏离量，正值表示平面是凸面，负值则为凹面；0.03125是常数值；在45⁰时COSθ等于0.70711，COS²θ等于0.5；△R是分别在垂直方向与水平方向切割时的差值；S是两块反射镜之间的距离，如图25.54所示。

用如下步骤测量△R值：将刀口调整到垂直切割方向，从上向下切割，直到得到均匀的阴影时，读出计数器的读数。然后，将刀口调整到水平方向，轴向移进或推出，直到阴影均匀时再次读数。如果刀口向里移动，读数为正值。

在操作过程中要求有次序地进行。首先总是在垂直方向切割，然后在水平方向切割。例如垂直方向切割时，读数为7895（由计数器读取），水平方向切割时读数为7875，则7895-7875=0.02英寸是负值。如果垂直读数为7895，水平读数为7875，则7895-7875=0.02英寸是正值。

由式（26-12）可求得平面的曲率。任何情况下公式中的常数均为0.03125，但平面的直径与被检球面的曲率半径比值的平方(D/R)²是变量。

当平面反射镜与光轴成45⁰时，COSθ/SIN²θ也是常数，等于0.70711/0.70711²=1.4142。

重要的在于精确地确定45⁰角。

如图26.54所示，角度倾角误差必须在1/4⁰以内。显然，倾斜角越大，能够检验的平面也就越大，而且检验灵敏度亦越高。

△R值是测量曲率中心的变化值。

对45⁰倾斜角，式（26-11）简化为：

h=0.03125×(D/R)²×1.4142×△R×R/(R-S)       (26-13)

例如：D=10英寸；R=240英寸；△R=0.2英寸；S=20英寸

代入后R/（R-S）=1.091和(D/R)²=0.01737，当已知△R=0.2英寸时，经多重乘积得：

h=0.03125×0.001736×1.4142×0.02×1.091=0.0000016英寸

用0.000021除之，则为0.076波长或近似地为1/10波长。这就是直径为10英寸平面的曲率。如果△R为负值，则平面为凹面；反之为凸面。

球面的直径应该比平面的直径大，使之口径能被充满，但计算时不涉及被检球面的直径。

分析到现在为止，仅得到一定直径D₁（水平直径）的一个方向的近似曲率。

下一步是要将刀口旋转90⁰，但决不能使球面装置走动，然后在垂直的直径方向对每个刀口位置作五次读数，再取其平均值。用与水平方向D₁的相同计算方法计算出新的90⁰方向D₂的近似曲率。

 

36．用象散焦点图计算△Rs的变化

因为不同平面内的曲率半径不同，所以只能得到直径D₁的近似曲率半径。第一种装置中的修正量是垂直与水平方向切割的差值。当刀口旋转90⁰至水平平面时，Ｖ等于第二次切割时的差值（见图26.55），也可以在两个直径方          图26.55检验象散时，反射镜的相对位置关系

向修正△Rs。

与球面成４５^０方向检验图形平面时，图26.55a呈椭园形。将平面反射镜作上记号，使之放入检验装置中的位置不变。b图是在短椭园平面上更长的Ｄ_２方向测量。a图是水平刀口切割时的初始位置，第二个椭园平面内曲率的差值形成象散焦点图。由式（２６－１４）可得出近似的变化。有关这方面内容在下一节再讨论。当刀口旋转９０^０成垂直方向切割时，还可给出一个不同直径方向的近似公式：

D₁=2H/3(+)V/3

D₂=H/3(+)2V/3                     (26-14)

式中Ｈ表示水平切割；Ｖ表示垂直切割。如果平面反射镜是理想的，则在两个走私方向切割时，在测量精度内的检测结果为零。反之，如果被检平面反射镜有１２－１５个波长的曲率误差，则检验结果与计算值的误差达一个波长左右。平面反射镜面形质量提高时，两者更为接近。如果误差小于0.25个波长，则为精确的结果。大多数的光学检验都有这种特性。

 

37． 新的△Rs

如图26.54a,b所示，假设在两个直径方向检验平面反射镜，并用刀口仪的计数器求△Rs值。下面举例说明之，Ｄ_１在水平方向切割时，△R值为0.02英寸，Ｄ_２在垂直方向切割时，是-0.005英寸。

由△R得D₁=2H/3(+)V/3 ,D₁=2×0.02/3-0.005/3=0.01(+)-0.0016=0.0084英寸。由△R求D₂=H/3（+）2V/3=0.02/3+2(-0.005)/3=0.006(+)-0.003=+0.003英寸。

将代入式（26-13），式中h=0.03125×0.001736×1.4142×△R×1.091。

当然，两个直径方向应该只有一个h值，如果两个h值有差别，则表示存在象散。例如上例D₁对应的h=0.03波长，D₂对应的h=-0.005波长，则象散等于0.025波长。

 

38．不规则形状的带差

检验不规则表面形状时，以前记住公式中的D值是在水平方向测量的。因此，如果用直径为8英寸的平面检验6英寸的表面时，D₁值应该是较小的直径方向，而D₂是较大的直径方向。由于45⁰方向（或其它角度方向）上产生缩小效应，观察时每个表面形成与直径成比例的一个椭园形，因此每个直径方向的校正位移量是相同的。

 

39．三次反射后环带误差的测量

平面的带差测量与前述的球面测量过程相同，但计算方法不同。用从左到右与从右向左的切割，找出水平直径方向上的最高点位置，只要在水平直径方向检测就可以了。计算公式为：

    h=y△RW/(2R)²         (26-15)

式中，h等于环带y处偏离总曲率的深度；W为环带的宽度；△R是水平截面内平均曲率中心与斜坡平均曲率中心之差值。

由两次或多次反射找出凸部或凹部并用软铅笔在平面上作一个记号。由于系统的视差，通过刀口可观察到两个象。

视差是由于光源与象分离而形成了第二个象的结果。当观察者面向装置，光源在光轴右边时，象在左侧，而第二个软铅笔记号象在其左边。对每个环带作两边切割时的环带轮廓是右边的象。这种双线效应说明刀口检验时需要把视差尽可能地减小。

例如分析直径为10英寸工件的塌边：

R=100英寸，标准球面的曲率半径；

W=1.5英寸，塌边宽度；

 Y=3.5英寸，与光轴相距为3.5+1.5或者在0.5D处测量时，△R为0.01英寸。

代入式（26-15）

    3.5×0.01×1.5/(2×10.000)=0.00000262英寸

用0.000021英寸除，其结果稍大于0.1波长。

在这个例子中，存在着翘边或中心与边缘之间的带区误差。处理三次反射进的唯一差别是计算式中的除数用2R²代之单次反射时的R²，同时可以用环带测量剖面图作为依据。

 

40．平面与抛物面的零位检验

共轴系统中的光学元件，在制造平面或抛物面过程中，可以用零位检验方法。这种方法有许多优点，而最主要的缺点是45⁰反射镜的阴影形成的中心死区。牛顿装置中，平面或抛物面中的通孔或者检验装置中准直镜上钻的通孔都是不通光的。第一个例子，45⁰反射镜在抛物面中心区域存在阴影。第二个例子中的孔使一部分准直光束用作检验。如果需要检验抛物面的全孔径，则要用离轴抛物面的方法（见图26.56）.

即使大的光学车间，也很少用离轴抛物面镜作为准直仪。6英寸离轴抛物面组成的准直仪是目前可供使用的最大准直镜，但价格昂贵。自从发明激光后，小型球轴承及镀银球的激光照明系统已经实用化（见附录16）。显然2mm细棒状托架的球形光源仅形成1’左右的中心阴影。                    图26.56  用穿孔的平面镜作检验

图26.56说明抛物面、平面、刀口、光源及阴影象的位置，TA表示检验时可以使用的区域，称之为“检验区”，W为“被检验的工件。

这种结构是紧凑的，在大多数情况下不需要助手，操作者可以自行调整工件。许多情况下，例如检验前工作面的工件、平行平板、直角棱镜或可以内反射平行光束的元件就不需要用平面镜M₂。为了检验玻璃的象质、均匀性或焦距，也不必用平面反射镜而只要将光源置于抛物面的轴上，以消除视差。

以后将要讨论检验消色差物镜的方法。消色差物镜中的平面反射镜起准直镜的作用。

分析图26.56发现该装置能够用于检验平面或抛物面。总之，不管作什么用途，每块反射镜都必须有极好的质量。

该方法中一个重要的问题是反射镜的准直调整，其平行度必须很好，即使小量的象散和慧差在精密加工中也是不允许的。

完成准直调整工作最简单的方法之一是在每块反射镜周边上系上粗而黑的十字丝。一根丝沿着垂直直径方向，另一根丝沿水平直径方向（见图26.57a和b）。用胶带纸或用实验室蜡将十字丝绷紧后粘在镜座上并使十字丝与表面尽可能靠近。

初步对准时，移开刀口，用一工作如灯照明反射镜表面。如果不准直，出现多于三外的十字线象，则佼准反射镜，直到十字线重合或靠拢。第一步做到这样就足够了。进行调整时，可能需要将一块反射镜沿着垂直光轴方向移动。如果检验如上缺少导轨，则用一支软铅笔在检验台上画出中心线。用与检验如的中心线同心，并正确地位于垂直直径上的垂直悬锤线来重新安置竖直的十字线。

要把几块反射镜的中心轴调整到同一标高平面上或相等高度。                  图26.57   十字线的安装

初调完成后，将刀口移到原来位置时应看见十字线和它的影子。这时视差的影响是明显的，要使所有的十字线和它影子重叠是不可能的。快调整完成时，可以减少它们的分离程度，使之只出现三对十字经。这可不必用特别的办法而用“切割和调整”形式进行调整即可。达到理想调整状态后，平面上的十字线影子位于抛物面上的十字线影子之间。

调整到某一阶段以后将出现二级和三级的衍射十字线阴影，一旦反射镜接近准直时，变不会出现这种阴影。

因为这里使用了精确调整的系统并用高质量零件作零位检测，所以切割一块高质量反射镜时可获得平滑而均匀的阴影。

用上述方法找出环带误差来指导修磨，并用10X目镜检验象质。

因为这类检验方法只用来检验不允许有环带误差或其它起伏不平的高质量表面，因而，用刀口和目镜检验法的目测结果，可以满足指导大多数具有关键要求的镜面修磨的需要。

 

参考文献：

Focault,L.M. “Description des Procedes Emplye pour Recommaitre la Configuration des Optiques,” C.R.Acad.Sci.Paris,47,958(1858): reprinted in Classques de la Science, Vol.II,Armand Colin.

Porter,R.W. “Mirror making for Reflecting Telescopes,” in Amateur Telescope Making, A.G.Ingalls, Ed.Munn,New York,1928,pp.1-19.

Strong,J. Procedures in Experimental Physics, Prentice-Hall, New York, 1943,pp.72-77.

Texerau, J. How to Make A Telescope, Doubleday,Garden City,NY,1963,pp.95-150.